前言

文章内容主要是对课程学习的一个总结，同时也是方便自己日后的复习和有需要人士的学习。

课程提纲

  1. Acwing1237.螺旋折线
  2. 双指针
    • 双指针模板
    • Acwing1238.日志统计
  3. BFS
    • BFS模板
    • Acwing1101.献给阿尔吉侬的花束
  4. 图论
    • Acwing1224.交换瓶子

Acwing1237.螺旋折线

题目

原题链接

如下图所示的螺旋折线经过平面上所有整点恰好一次。

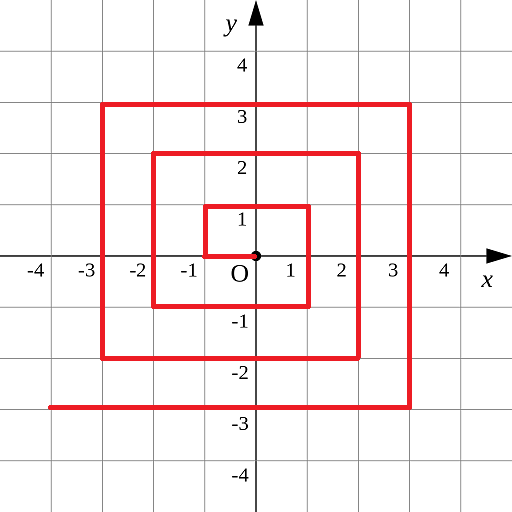
对于整点 (X,Y)，我们定义它到原点的距离 dis(X,Y) 是从原点到 (X,Y) 的螺旋折线段的长度。

例如 dis(0,1)=3,dis(−2,−1)=9

给出整点坐标 (X,Y)，你能计算出 dis(X,Y) 吗？
输入格式
包含两个整数 X,Y。

输出格式
输出一个整数，表示 dis(X,Y)。

数据范围
−10^9 ≤ X,Y ≤ 10^9

输入样例：

1
0 1

输出样例:

1
3

分析

对于上面这样一道题，我们首先想到的应该是模拟。但由于题目所给的数据范围较大，如果采用直接模拟的方式，大概率是超时的，但也能够在比赛中取得一个比较不错的分数。从数据范围我们也不难发现，这应该是一道找规律的题目。为此我们给图上的每个点进行标注，可以得到如下的规律。

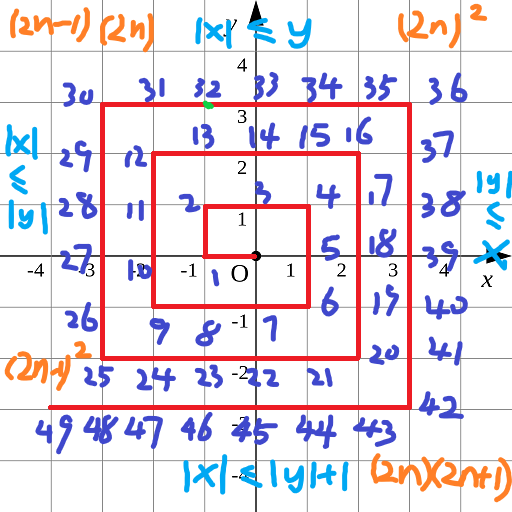
由此，我们不难写出以下代码。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int x,y;
int main()
{
    cin >> x >> y;
    if(abs(x) <= y)
    {
        int n = y;
        cout << (LL)(2 * n - 1) * (2 * n) + x - (-n) << endl;
    }else if(abs(y) <= x)
    {
        int n = x;
        cout << (LL)(2 * n) * (2 * n) + (n - y) << endl;
    }else if(abs(x) <= abs(y) + 1 && y < 0)
    {
        int n = abs(y);
        cout << (LL)(2 * n) * (2 * n + 1) + (n - x) << endl;
    }else
    {
        int n = abs(x);
        cout << (LL)(2 * n - 1) * (2 * n - 1) + y - (-n + 1) << endl;
    }
    return 0;
}

Acwing1238.日志统计

题目

原题链接

小明维护着一个程序员论坛。现在他收集了一份”点赞”日志，日志共有 N 行。

其中每一行的格式是：

ts id

表示在 ts 时刻编号 id 的帖子收到一个”赞”。

现在小明想统计有哪些帖子曾经是”热帖”。

如果一个帖子曾在任意一个长度为 D 的时间段内收到不少于 K 个赞，小明就认为这个帖子曾是”热帖”。

具体来说，如果存在某个时刻 T 满足该帖在 [T,T+D) 这段时间内(注意是左闭右开区间)收到不少于 K 个赞，该帖就曾是”热帖”。

给定日志，请你帮助小明统计出所有曾是”热帖”的帖子编号。

输入格式
第一行包含三个整数 N,D,K。

以下 N 行每行一条日志，包含两个整数 ts 和 id。

输出格式
按从小到大的顺序输出热帖 id。

每个 id 占一行。

数据范围
1 ≤ K ≤ N ≤ 10^5,
0 ≤ts,id≤ 10^5,
1 ≤ D ≤ 10000

输入样例:

1
2
3
4
5
6
7
8
7 10 2
0 1
0 10
10 10
10 1
9 1
100 3
100 3

输出样例:

1
2
1
3

分析

读题后我们可以发现，通过遍历长度为D的时间段，并每次统计时间段内id的获赞数， 当cnt>=K时进行标记即可得到所求结果。但实现代码后，时间复杂度为O（N * D），题目给出的数据范围经计算后会超时，所以我们需要继续优化。对于每个时间段统计的获赞数，我们发现实际上有很多重复的部分，在时间段移动的过程中，日志记录只会变化前后一段，为此我们可以使用双指针进行优化。由此，我们不难写出以下代码。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
typedef pair<int,int> PII;
int n,d,k;
PII logs[N];
int cnt[N];
bool st[N];
int main()
{
    cin >> n >> d >> k;
    for(int i = 0;i < n;i++) cin >> logs[i].first >> logs[i].second;
    sort(logs,logs + n);
    for(int i = 0,j = 0;i < n;i++)
    {
        int id = logs[i].second;
        //当前id的日志数量+1
        cnt[id]++;
        //删掉之前超出时间段的日志
        while(logs[i].first - logs[j].first >= d)
        {
            cnt[logs[j].second]--;
            j++;
        }
        if(cnt[id] >= k) st[id] = true;
    }
    for(int i = 0;i < 100005;i++) if(st[i]) cout << i << endl;
    return 0;
}

Acwing1101.献给阿尔吉侬的花束

题目

原题链接

阿尔吉侬是一只聪明又慵懒的小白鼠，它最擅长的就是走各种各样的迷宫。

今天它要挑战一个非常大的迷宫，研究员们为了鼓励阿尔吉侬尽快到达终点，就在终点放了一块阿尔吉侬最喜欢的奶酪。

现在研究员们想知道，如果阿尔吉侬足够聪明，它最少需要多少时间就能吃到奶酪。

迷宫用一个 R×C 的字符矩阵来表示。

字符 S 表示阿尔吉侬所在的位置，字符 E 表示奶酪所在的位置，字符 # 表示墙壁，字符 . 表示可以通行。

阿尔吉侬在 1 个单位时间内可以从当前的位置走到它上下左右四个方向上的任意一个位置，但不能走出地图边界。

输入格式
第一行是一个正整数 T，表示一共有 T 组数据。

每一组数据的第一行包含了两个用空格分开的正整数 R 和 C，表示地图是一个 R×C 的矩阵。

接下来的 R 行描述了地图的具体内容，每一行包含了 C 个字符。字符含义如题目描述中所述。保证有且仅有一个 S 和 E。

输出格式
对于每一组数据，输出阿尔吉侬吃到奶酪的最少单位时间。

若阿尔吉侬无法吃到奶酪，则输出“oop!”（只输出引号里面的内容，不输出引号）。

每组数据的输出结果占一行。

数据范围
1< T ≤ 10,
2 ≤ R,C ≤ 200

输入样例：

1
2
3
4
5
6
7
8
9
10
11
12
13
3
3 4
.S..
###.
..E.
3 4
.S..
.E..
....
3 4
.S..
####
..E.

输出样例：

1
2
3
5
1
oop!

分析

这题本质上就是一个简单的棋盘BFS模型，BFS一般有两种模型：棋盘模型和状态模型，那么万变不离其宗还是套BFS模板，由此，根据题意进行转换，我们不难写出以下代码。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> PII;
const int N = 210;
int T;
char g[N][N];
int dist[N][N];
int n,m;
int bfs(PII start,PII end)
{
    queue<PII> q;
    q.push(start);
    memset(dist,-1,sizeof dist);
    dist[start.first][start.second] = 0;
    int dx[4] = {-1,0,1,0},dy[4] = {0,1,0,-1};
    while(q.size())
    {
        auto t = q.front();
        if(end == t) return dist[end.first][end.second];
        q.pop();
        for(int i = 0;i < 4;i++)
        {
            int x = t.first + dx[i],y = t.second + dy[i];
            if(x < 0 || x >= n || y < 0 || y >= m) continue;
            if(g[x][y] == '#') continue;
            if(dist[x][y] != -1) continue;
            dist[x][y] = dist[t.first][t.second] + 1;
            q.push({x,y});
        }
    }
    return -1;
}
int main()
{
    cin >> T;
    while(T--)
    {
        PII start,end;
        cin >> n >> m;
        for(int i = 0;i < n;i++)
        {
            for(int j = 0;j < m;j++)
            {
                cin >> g[i][j];
                if(g[i][j] == 'S') start = {i,j};
                else if(g[i][j] == 'E') end = {i,j};
            }
        }
        int t = bfs(start,end);
        if(t == -1) cout << "oop!" << endl;
        else cout << t << endl;
    }
    
    return 0;
}

Acwing1224.交换瓶子

题目

原题链接

有 N 个瓶子，编号 1∼N，放在架子上。

比如有 5 个瓶子：

2 1 3 5 4
要求每次拿起 2 个瓶子，交换它们的位置。

经过若干次后，使得瓶子的序号为：

1 2 3 4 5
对于这么简单的情况，显然，至少需要交换 2 次就可以复位。

如果瓶子更多呢？你可以通过编程来解决。

输入格式
第一行包含一个整数 N，表示瓶子数量。

第二行包含 N 个整数，表示瓶子目前的排列状况。

输出格式
输出一个正整数，表示至少交换多少次，才能完成排序。

数据范围
1 ≤ N ≤ 10000,

输入样例1：

1
2
5
3 1 2 5 4

输出样例1：
1
3

输入样例2：
1
2
5
5 4 3 2 1

输出样例2：
1
2

分析

这题本身是一道很经典的题目，思维非常巧妙，尽管它归属图论部分，也只是因为它的本质用到了图论的置换群。我们将每个数字与它应在位置的数字连一条边，可得到如下的图。

并且我们可以发现，交换一对环内的数字，就是将两条边的方向置换，即将一个环拆分成两个环；交换一对环外的数字，也是将两条边的方向置换，但是将两个环合并成一个环。

假定有k个这样的环，我们会发现，通过这两种操作，至少只需要n - k次就可以将所有的数字变为自环。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int n;
bool st[N];
int main()
{
    cin >> n;
    for(int i = 1;i <= n;i++) cin >> a[i];
    int cnt = 0;
    for(int i = 1;i <= n;i++)
    {
        if(!st[i])
        {
            cnt++;
            for(int j = i;!st[j];j = a[j]) st[j] = true;
        }
    }
    cout << n - cnt << endl;
    return 0;
}